This tutorial will use the K-nearest neighbors (KNN) algorithm to predict the number of points NBA players scored in the 2013–2014 season. We will also explore the concept of Euclidean distance and determine which NBA players are most similar to Lebron James. You can download the dataset in CSV format from the provided link.
Understanding the Dataset
Before we delve into the algorithm, let’s familiarize ourselves with the dataset. Each row in the dataset provides information about a player’s performance during the 2013–2014 NBA season.
Here are some key columns from the dataset:
player: Player’s namepos: Player’s positiong: Number of games the player participated ings: Number of games the player startedpts: Total points the player scored
The dataset contains many other columns, primarily detailing the average performance of a player over the season. For a detailed explanation of these columns, refer to the provided link.
Let’s load our dataset and identify the available columns:
import pandas as pd
with io.open("nba_13.csv") as csvfile:
nba = pd.read_csv(csvfile)
print(nba.columns.values)
Overview of KNN
The K-nearest neighbors (KNN) algorithm predicts unknown values by comparing them with the most similar known values.
Consider an example where we have data about three different types of cars. We know the car’s name, its horsepower, whether it has racing stripes, and whether it’s fast:
Sure, here’s the data presented in a table format:
Now, suppose we have another car, but we don’t know whether it’s fast:
Here’s the data you provided in a table format:
To predict whether this car is fast, we use KNN to find the most similar known car. We compare the horsepower and racing_stripes values and find that the most similar car is the Yugo. Since the Yugo is fast, we predict that the Camaro is also fast. This is an example of 1-nearest neighbor, where we only look at the most similar car, giving us a k of 1.
If we used 2-nearest neighbors, we would consider the two most similar cars, the Delorean and the Yugo. Both are fast, so we predict the Camaro is also fast. This gives us a k of 2.
If we used 3-nearest neighbors, we would consider the Honda Accord in addition to the Delorean and the Yugo. This would give us two True values and one False value, averaging out to True.
The number of neighbors (k) we use for KNN can be any value less than the number of rows in our dataset. However, in practice, considering only a few neighbors often yields better results because the less similar the neighbors are to our data, the less accurate the prediction will be.
Understanding Euclidean Distance
Before making predictions using the KNN algorithm, we need to determine which data rows are “closest” to the row we’re trying to predict. A straightforward way to do this is by using Euclidean distance. The formula for Euclidean distance is:
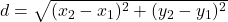
For instance, consider these two rows (where True/False has been converted to 1/0), and we want to find the distance between them:
car,horsepower,is_fast
Honda Accord,180,0
Chevrolet Camaro,400,1
We first select only the numeric columns. Then the distance becomes:
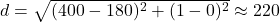
We can apply the concept of Euclidean distance to find NBA players most similar to Lebron James.
# Select Lebron James from our dataset
selected_player = nba[nba["player"] == "LeBron James"].iloc[0]
# Choose only the numeric columns (we'll use these to compute euclidean distance)
distance_columns = ['age', 'g', 'gs', 'mp', 'fg', 'fga', 'fg%', '3p', '3pa', '3p%', '2p', '2pa', '2p%', 'efg%', 'ft', 'fta', 'ft%', 'orb', 'drb', 'trb', 'ast', 'stl', 'blk', 'tov', 'pf', 'pts']
import math
def euclidean_distance(row):
""" A simple euclidean distance function """
inner_value = 0 for k in distance_columns: inner_value += (row[k] - selected_player[k]) ** 2
return math.sqrt(inner_value)
# Find the distance from each player in the dataset to Lebron.
lebron_distance = nba.apply(euclidean_distance, axis=1)
print(lebron_distance)
0 48.769017 1 45.788337 2 22.325645 3 78.102996 4 53.789402 ... 807 74.949319 808 32.790107 809 63.603606 810 77.528591 811 44.858014 Length: 812, dtype: float64
Normalizing Features
In the car example, you may have noticed that the ‘horsepower’ had a much larger impact on the final distance than ‘is_fast’. This is because the values of ‘horsepower’ are much larger, thus overshadowing the impact of ‘is_fast’ in the Euclidean distance calculations.
This can be problematic because a variable with larger values doesn’t necessarily make it better at predicting similar rows.
A simple solution is to normalize all the features with a mean of 0 and a standard deviation of 1. This ensures that no single column has a dominant impact on the Euclidean distance calculations.
To set the mean to 0, we find the mean of a column and subtract it from every value in the column. To set the standard deviation to 1, we divide every value in the column by the standard deviation. The formula is:
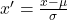
# Select only the numeric columns from the NBA dataset
nba_numeric = nba[distance_columns]
# Normalize all of the numeric columns
nba_normalized = (nba_numeric - nba_numeric.mean()) / nba_numeric.std()
Finding the Nearest Neighbor
We are now equipped to find the nearest neighbor of a given row in the NBA dataset. We can use the distance.euclidean function from scipy.spatial, which is a faster way to calculate Euclidean distance.
from scipy.spatial import distance
# Fill in NA values in nba_normalized
# We use squeeze() to convert the resulting DataFrame into a Series for compatibility with distance.euclidean nba_normalized.fillna(0, inplace=True) # Find the normalized vector for Lebron James.
lebron_normalized = nba_normalized[nba["player"] == "LeBron James"].squeeze()
# Find the distance between Lebron James and everyone else.
euclidean_distances = nba_normalized.apply(lambda row: distance.euclidean(row, lebron_normalized), axis=1)
# Create a new dataframe with distances.
distance_frame = pd.DataFrame(data={"dist": euclidean_distances, "idx": euclidean_distances.index}) distance_frame.sort_values("dist", inplace=True)
# Find the most similar player to Lebron (the lowest distance to Lebron is Lebron, the second smallest is the most similar non-Lebron player)
second_smallest = distance_frame.iloc[1]["idx"]
most_similar_to_lebron = nba.loc[int(second_smallest)]["player"]
In this code, we first fill in any NA values in nba_normalized with 0. Then, we find the normalized vector for Lebron James and calculate the Euclidean distance between Lebron James and every other player. We create a new dataframe with these distances, sort it, and find the player most similar to Lebron James.
Creating Training and Testing Sets
We first need to generate training and testing sets to make predictions on a test set using the nearest neighbors. We’ll aim to predict a player’s scored points using the five closest neighbors, considering all the numeric columns in the dataset to generate similarity scores.
We’ll use random sampling to create these sets. We’ll randomly shuffle the index of the nba dataframe and select rows using these shuffled values. If we don’t do this, we would predict and train on the same dataset, leading to overfitting. While we could also use cross-validation, which might yield slightly better results, it’s also slightly more complex.
import random from numpy.random
import permutation
import math # Randomly shuffle the index of nba. random_indices = permutation(nba.index) # Set a cutoff for how many items we want in the test set (in this case 1/3 of the items)
test_cutoff = math.floor(len(nba)/3) # Generate the test set by taking the first 1/3 of the randomly shuffled indices. test = nba.loc[random_indices[1:test_cutoff]] # Generate the train set with the rest of the data.
train = nba.loc[random_indices[test_cutoff:]]
Using Scikit-Learn for K-Nearest Neighbors
Instead of doing everything manually, we can use the k-nearest neighbors implementation in scikit-learn. Scikit-learn automatically normalizes the data and calculates distances, allowing us to specify how many neighbors we want to consider.
# The columns that we will be making predictions
with.
x_columns = ['age', 'g', 'gs', 'mp', 'fg', 'fga', 'fg.', 'x3p', 'x3pa', 'x3p.', 'x2p', 'x2pa', 'x2p.', 'efg.', 'ft', 'fta', 'ft.', 'orb', 'drb', 'trb', 'ast', 'stl', 'blk', 'tov', 'pf']
# The column that we want to predict.
y_column = ["pts"]
from sklearn.neighbors import KNeighborsRegressor
# Create the knn model.
# Look at the five closest neighbors.
knn = KNeighborsRegressor(n_neighbors=5)
# Fit the model on the training data.
knn.fit(train[x_columns], train[y_column])
# Make point predictions on the test set using the fit model.
predictions = knn.predict(test[x_columns])
Calculating Error
Now that we have our point predictions, we can calculate the error associated with our predictions. We can compute the mean squared error (MSE), which is given by the formula:
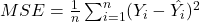
Where Y_i is the actual value, hat{Y_i} is the predicted value, and (n) is the number of data points.
# Get the actual values for the test set.
actual = test[y_column]
# Compute the mean squared error of our predictions.
mse = (((predictions - actual) ** 2).sum()) / len(predictions)
Conclusion
In this tutorial, we explored how to use the K-nearest neighbors algorithm to predict NBA player performance. We learned how to prepare our data, normalize columns, and generate training and testing sets. We also used the scikit-learn library to simplify the process of finding the nearest neighbors and making predictions. Finally, we calculated the mean squared error to evaluate the accuracy of our predictions. This approach provides a practical way to make predictions on continuous data and can be applied to a wide range of problems in data analysis and machine learning.
The Jupyter Notebook for this tutorial is available for download here.